Tensoranalyse, matematikgren, der beskæftiger sig med relationer eller love, der forbliver gyldige uanset systemet med koordinater, der bruges til at specificere mængderne. Sådanne forhold kaldes covariant. Tensorer blev opfundet som en udvidelse af vektorer for at formalisere manipulationen af geometriske enheder, der opstod i studiet af matematiske manifolds.
En vektor er en enhed, der har både størrelse og retning; det kan repræsenteres ved en tegning af en pil, og den kombineres med lignende enheder i henhold til parallelogramloven. På grund af denne lov har en vektor komponenter — et andet sæt for hvert koordinatsystem. Når koordinatsystemet ændres, ændres vektorens komponenter i henhold til en matematisk transformationslov, der kan afledes fra parallelogramloven. Denne lov om transformation af komponenterne har to vigtige egenskaber. Først efter en række ændringer, der ender i det originale koordinatsystem, vil vektorens komponenter være de samme som ved starten. For det andet vil forhold mellem vektorer - for eksempel tre vektorer U, V, W, således at 2U + 5V = 4W - være til stede i komponenterne uanset koordinatsystemet.
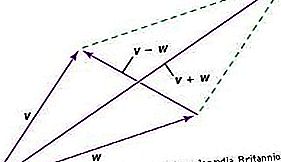
En vektor kan derfor betragtes som en enhed, der i n-dimensionelt rum har n komponenter, der transformerer i henhold til en specifik transformationslov med ovennævnte egenskaber. Selve vektoren er en objektiv enhed uafhængig af koordinater, men den behandles med hensyn til komponenter med alle koordinatsystemer på lige fod.
Uden at insistere på et billedbillede defineres en tensor som en objektiv enhed, der har komponenter, der ændrer sig i henhold til en transformationslov, der er en generalisering af den vectoriale transformation, men som bevarer de to centrale egenskaber ved denne lov. For nemheds skyld nummereres koordinaterne fra 1 til n, og hver komponent i en tensor er betegnet med et bogstav med superskripter og underskrifter, som hver uafhængigt påtager sig værdierne 1 til n. Således er en tensor repræsenteret af komponenterne T ab c ville have n 3 komponenter som værdierne af a, b og c løber fra 1 til n. Scalarer og vektorer udgør særlige tilfælde af tensorer, hvor førstnævnte kun har en komponent pr. Koordinatsystem og sidstnævnte besidder n. Enhver lineær forbindelse mellem tensorkomponenter, såsom7R a bcd + 2S a bcd - 3T a bcd = 0, hvis den er gyldig i et koordinatsystem, er gyldig i alt og repræsenterer således et forhold, der er objektivt og uafhængigt af koordinatsystemer på trods af mangel på en billedlig repræsentation.
To tensorer, kaldet den metriske tensor og krumningstensoren, er af særlig interesse. Den metriske tensor bruges for eksempel til konvertering af vektorkomponenter til størrelser af vektorer. For enkelheds skyld skal du overveje den todimensionelle sag med enkle vinkelrette koordinater. Lad vektor V har komponenterne V 1, V 2. Derefter ved hjælp af den Pythagoreiske teorem, der er anvendt på den højre trekant OAP, kvadratet med størrelsen af V er givet vedOP 2 = (V 1) 2 + (V 2) 2.

Skjult i denne ligning er den metriske tensor. Det er skjult, fordi det her består af 0'er og 1'er, der ikke er skrevet i. Hvis ligningen omskrives i formOP 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, er det fulde sæt af komponenter (1, 0, 0, 1) i den metriske tensor tydeligt. Hvis der anvendes skrå koordinater, tager formlen for OP 2 den mere generelle formOP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, mængderne g 11, g 12, g 21, g 22 er de nye komponenter i den metriske tensor.
Ud fra den metriske tensor er det muligt at konstruere en kompliceret tensor, kaldet krumningstensor, der repræsenterer de forskellige aspekter af den iboende krumning i det n-dimensionelle rum, som det hører til.
Tensorer har mange anvendelser inden for geometri og fysik. Ved at skabe sin generelle relativitetsteori argumenterede Albert Einstein for, at fysiklovene skal være de samme, uanset hvilket koordinatsystem der bruges. Dette førte til, at han udtrykte disse love med hensyn til tensor-ligninger. Det blev allerede kendt fra hans specielle relativitetsteori, at tid og rum hænger så tæt sammen, at de udgør en udelelig fire-dimensionel rumtid. Einstein postulerede, at gravitationen udelukkende skulle repræsenteres med hensyn til den metriske tensor i firdimensionel rumtid. For at udtrykke den relativistiske tyngdelov havde han som byggeblokke den metriske tensor og krumningstensoren dannet ud fra den. Da han først besluttede at begrænse sig til disse byggesten, førte deres meget vanskelighed ham til en i det væsentlige unik tensor ligning for gravitationsloven, hvor gravitationen ikke fremkom som en kraft, men som en manifestation af rumtidens krumning.
Mens tensorer var blevet undersøgt tidligere, var det succes med Einsteins generelle relativitetsteori, der gav anledning til den aktuelle udbredte interesse hos matematikere og fysikere i tensorer og deres anvendelser.