Konisk snit, også kaldet kegle, i geometri, enhver kurve produceret ved skæringspunktet mellem et plan og en højre cirkulær kegle. Afhængigt af planets vinkel i forhold til keglen, er skæringspunktet en cirkel, en ellipse, en hyperbola eller en parabola. Særlige (degenererede) tilfælde af krydsning forekommer, når flyet kun passerer gennem spidsen (producerer et enkelt punkt) eller gennem spidsen og et andet punkt på keglen (der producerer en lige linje eller to krydsende lige linjer). Se figuren.
projektiv geometri: Projektive keglesnit
Koniske sektioner kan betragtes som plane sektioner af en højre cirkulær kegle (se figuren). Ved at betragte
De grundlæggende beskrivelser, men ikke navnene, på keglesektionerne kan spores til Menaechmus (blomstret ca. 350 f.Kr.), en elev af både Platon og Eudoxus fra Cnidus. Apollonius fra Perga (ca. 262-190 f.Kr.), kendt som ”Det store geometer”, gav keglesektionerne deres navne og var den første til at definere de to grene af hyperbola (som forudsætter dobbeltkeglen). Apollonius 'otte-bindende afhandling om keglesektionerne, Conics, er et af de største videnskabelige værker fra den antikke verden.
Analytisk definition
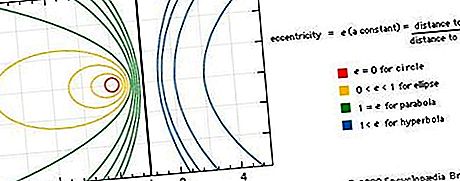
Koniske kan også beskrives som plane kurver, der er stierne (loci) for et punkt, der bevæger sig, så forholdet mellem dets afstand fra et fast punkt (fokus) og afstanden fra en fast linje (directrix) er en konstant, kaldet kurvens excentricitet. Hvis excentriciteten er nul, er kurven en cirkel; hvis lig med en, en parabola; hvis mindre end en, en ellipse; og hvis større end en, en hyperbola. Se figuren.
Hvert konisk snit svarer til grafen for en polynomial ligning i anden grad af formen Ax 2 + By 2 + 2Cxy + 2Dx + 2Ey + F = 0, hvor x og y er variabler og A, B, C, D, E og F er koefficienter, der afhænger af den særlige koniske. Ved passende valg af koordinatakser, kan ligningen for enhver keglesnit reduceres til en af tre simple r former: x 2 / a 2 + y 2 / b 2 = 1, x 2 / a 2 - y 2 / b 2 = 1 eller y 2 = 2 px, svarende til henholdsvis en ellipse, en hyperbola og en parabola. (En ellipse, hvor a = b faktisk er en cirkel.) Den omfattende anvendelse af koordinatsystemer til den algebraiske analyse af geometriske kurver stammer fra René Descartes (1596–1650). Se Historie om geometri: Cartesian geometry.
Græsk oprindelse
Den tidlige historie med koniske sektioner er forbundet med problemet med "at fordoble terningen." Ifølge Eratosthenes fra Cyrene (ca. 276-190 f.Kr.) konsulterede befolkningen i Delos oraklet af Apollo for at få hjælp til at afslutte en pest (ca. 430 f.Kr.) og blev instrueret om at bygge Apollo et nyt alter på det dobbelte af det gamle alterets volumen og med samme kubikform. Forvirrende rådførte Delianerne sig med Platon, der sagde, at ”orakelet ikke betød, at guden ville have et alter af dobbelt størrelse, men at han ønskede at sætte dem til opgaven at skamme grækerne for deres forsømmelse af matematik og deres foragt til geometri. ” Hippokrates of Chios (ca. 470–410 bc) opdagede først, at ”Delian-problemet” kan reduceres til at finde to gennemsnitlige proportioner mellem a og 2a (mængderne af de respektive altere) - det er at bestemme x og y sådan, at en: x = x: y = y: 2a. Dette er ækvivalent med at løse samtidigt to af ligningerne x 2 = ay, y 2 = 2ax og xy = 2a 2, der svarer til henholdsvis to parabolas og en hyperbola. Senere viste Archimedes (ca. 290-211 bc), hvordan man bruger koniske sektioner til at opdele en kugle i to segmenter med et givet forhold.
Diokler (ca. 200 f.Kr.) demonstrerede geometrisk, at stråler - for eksempel fra solen - der er parallelle med aksen for en paraboloid af revolution (produceret ved at dreje en parabola om dens symmetriakse) mødes i fokus. Det siges, at Archimedes har brugt denne ejendom til at sætte fjendtlige skibe i brand. Ellipsens fokale egenskaber blev citeret af Anthemius fra Tralles, en af arkitekterne for Hagia Sophia-katedralen i Konstantinopel (afsluttet i annonce 537), som et middel til at sikre, at et alter kunne oplyses med sollys hele dagen.