Permutationer og kombinationer matematik

Permutationer og kombinationer, de forskellige måder, hvorpå objekter fra et sæt kan vælges, generelt uden udskiftning, til at danne undergrupper. Dette valg af undergrupper kaldes en permutation, når rækkefølgen af ​​markering er en faktor, en kombination, når ordre ikke er en faktor. Ved at overveje forholdet mellem antallet af ønskede undergrupper og antallet af alle mulige undergrupper til mange tilfældighedsspil i det 17. århundrede gav de franske matematikere Blaise Pascal og Pierre de Fermat drivkraft til udviklingen af ​​kombinatorik og sandsynlighedsteori.

combinatorics: Binomiale koefficienter

n objekter kaldes en permutation af n ting taget r ad gangen. Antallet af permutationer er

Begreberne og forskellene mellem permutationer og kombinationer kan illustreres ved at undersøge alle de forskellige måder, hvorpå et par objekter kan vælges blandt fem adskilte objekter - såsom bogstaverne A, B, C, D og E. Hvis begge de valgte bogstaver og rækkefølgen af ​​markering tages i betragtning, så er følgende 20 resultater mulige:

Hver af disse 20 forskellige mulige valg kaldes en permutation. Især kaldes de permutationer af fem objekter taget to ad gangen, og antallet af sådanne mulige permutationer betegnes med symbolet ₅ P ₂, læses "5 permut 2." Generelt, hvis der er n objekter tilgængelige, hvorfra man kan vælge, og der skal dannes permutationer (P) ved hjælp af k af objekter ad gangen, angives antallet af forskellige mulige permutationer med symbolet _n P _k. En formel til evaluering heraf er _n P _k = n! / (N - k)! Udtrykket n! —Læst “n factorial” - angiver, at alle på hinanden følgende positive heltal fra 1 til og med n skal multipliceres sammen, og 0! er defineret til lig 1. Brug af denne formel er antallet af permutationer af fem objekter taget to ad gangen for eksempel

(For k = n, _n P _k = n! Så for 5 objekter er der 5! = 120 arrangementer.)

For kombinationer vælges k-objekter fra et sæt n-objekter til at producere delmængder uden at bestille. I modsætning til det forrige permutationseksempel med den tilsvarende kombination er AB- og BA-undergrupperne ikke længere forskellige valg; ved at eliminere sådanne tilfælde forbliver der kun 10 forskellige mulige undergrupper - AB, AC, AD, AE, BC, BD, BE, CD, CE og DE.

Antallet af sådanne undergrupper er angivet med _n C _k, læs "n vælg k." For kombinationer, da k objekter har k! arrangementer, der er k! uskilte permutationer for hvert valg af k-objekter; derfor dividerer permutationsformlen med k! giver følgende kombinationsformel:

Dette er det samme som den (n, k) binomiale koefficient (se binomial sætning). For eksempel er antallet af kombinationer af fem objekter taget to ad gangen

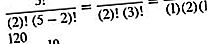
Formlerne for _n P _k og _n C _k kaldes tælleformler, da de kan bruges til at tælle antallet af mulige permutationer eller kombinationer i en given situation uden at skulle liste dem alle.