Euklids vindmølle

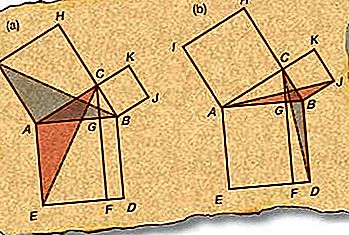
Pythagoræas sætning siger, at summen af ​​firkanterne på benene i en højre trekant er lig med kvadratet på hypotenusen (siden modsat den rigtige vinkel) - i kendt algebraisk notation, a ² + b ² = c ². Babylonierne og egypterne havde fundet nogle heltal tre (a, b, c) tilfredsstillende forholdet. Pythagoras (ca. 580 - ca. 500 f.Kr.) eller en af ​​hans tilhængere kan have været den første til at bevise det teorem, der bærer hans navn. Euclid (ca. 300 f.Kr.) bød på en smart demonstration af Pythagorean-sætningen i hans Elements, kendt som vindmølle-beviset fra figurens form.

1. Tegn firkanter på siderne af højre ΔABC.

2. BCH og ACK er lige linjer, fordi ∠ACB = 90 °.

3. ∠EAB = ∠CAI = 90 °, efter konstruktion.

4. ∠BAI = ∠BAC + ∠CAI = ∠BAC + ∠EAB = ∠EAC, med 3.

5. AC = AI og AB = AE, efter konstruktion.

6. Derfor, ΔBAI ≅ ΔEAC, ved sidevinkel-side teorem (se Sidebar: Bridge of Asses), som fremhævet i del (a) af figuren.

7. Træk CF parallelt med BD.

8. Rektangel AGFE = 2ΔACE. Dette bemærkelsesværdige resultat stammer fra to foreløbige teoremer: (a) arealerne af alle trekanter på den samme base, hvis tredje toppunkt ligger overalt på en ubestemt udvidet linje parallelt med basen, er lige; og (b) arealet af en trekant er halvdelen af ​​det for ethvert parallelogram (inklusive ethvert rektangel) med den samme base og højde.

9. Firkantet AIHC = 2ΔBAI ved det samme parallelograms sætning som i trin 8.

10. Derfor rektangel AGFE = firkantet AIHC ved trin 6, 8 og 9.

11. ∠DBC = ∠ABJ, som i trin 3 og 4.

12. BC = BJ og BD = AB ved konstruktion som i trin 5.

13. ΔCBD ≅ ΔJBA, som i trin 6 og fremhævet i del (b) af figuren.

14. Rektangel BDFG = 2ΔCBD, som i trin 8.

15. Firkantet CKJB = 2ΔJBA, som i trin 9.

16. Derfor rektangel BDFG = firkantet CKJB, som i trin 10.

17. Firkantet ABDE = rektangel AGFE + rektangel BDFG, efter konstruktion.

18. Derfor er kvadrat ABDE = firkant AIHC + firkant CKJB ved trin 10 og 16.

    Den første bog med Euclids elementer begynder med definitionen af ​​et punkt og slutter med det Pythagoreiske teorem og dets omvendte (hvis summen af ​​firkanterne på to sider af en trekant er lig med kvadratet på den tredje side, skal det være en højre trekant). Denne rejse fra særlig definition til abstrakt og universel matematisk udsagn er blevet taget som symbolsk for udviklingen af ​​det civiliserede liv. Et slående eksempel på identifikationen af ​​Euclids ræsonnement med det højeste tankegang var forslaget fra 1821 af en tysk fysiker og astronom om at åbne en samtale med indbyggerne i Mars ved at vise dem vores påstande om intellektuel modenhed. Alt hvad vi havde brug for at gøre for at tiltrække deres interesse og godkendelse, blev det hævdet, var at pløje og plante store marker i form af vindmøllediagrammet eller, som andre foreslog, at grave kanaler, der antyder Pythagoras sætning i Sibirien eller Sahara, fyld dem med olie, tænd dem og vent på et svar. Eksperimentet er ikke blevet forsøgt, hvilket efterlader ubestemt, om indbyggerne i Mars ikke har noget teleskop, ingen geometri eller ingen eksistens.